Four things come not back: the spoken word; the sped arrow; time post; the neglected opportunity.-Al Halif Omar Ibn
Introduction
The effort in ac circuit analysis so far has been focused mainly on calculating volatage and current. Our major concern in this chapter is power analysis.
Power analysis is of paramount importance. Power is the most important quantity in electric utilities, electronics, and communication system, because such systems involve transmission of power from one point to another. Also, every industrial household electrical device - every fan, motor, lamp, pressing iron, TV, personal computer - has a power rating that indicates how much power the equipment requires; exceeding the power rating can do permanent damage to an appliance. The most common form of electric power is 50- or 60- Hz ac power. The choice of ac cover dc allowed high-voltage power transmission from the power generating plant to the consumer.
We will begin by defining and deriving instantaneous power and average power. We will then introduce other power concepts. As practical applications of these concepts, we will discuss how power is measured and reconsider how electric utility companies charge their customers.
11.1 Instantaneous and Average Power
As mentioned in Chapter 2, the instantaneous power p(t) absorbed by an element is the product of the instantaneous voltage v(t) across the element and the instantaneous current i(t) through it. Assuming the passive convention.
p(t) = v(t)i(t) (11.1)
The instantaneous power (in watts) is the power at any instant of time.
- We can also think of the instantaneous power as the power absorbed by the element at a specific instant of time. Instantaneous quantities are denoted by lowercase letters.
It is the rate at which an element absorbs energy.
The average power (in watts) is the average of the instantaneous power over one period.
Real or average power: P can be defined in two ways: as the real part of the complex power or as the simple average of the instantaneous power. The second definition is more general because with it we can define the instantaneous power for any signal waveform, not just for sinusoids. It is given explicitly in the following expression


11.2 Maximun Average Power Transfer
INTRODUCTION
To obtain the maximum average power transferred from a source to a load, the load impedance should be chosen equal to the conjugate of the Thevenin equivalent impedance representing the reminder of the network.




INTRODUCTION
To obtain the maximum average power transferred from a source to a load, the load impedance should be chosen equal to the conjugate of the Thevenin equivalent impedance representing the reminder of the network.
11.3 Apparent Power and Power Factor
The apparent power (in VA) of the rms values of voltage and current.
Apparent power in S is the product of the rms values of the voltage and the current, S = U*I. The unit of apparent power is VA. The apparent power is the absolute value of the complex power, so it is defined only for sinusoidal excitation.
The Power Factor (cos φ) is the cosine of the phase difference between voltage and current. It is also the cosine of the angle of the load impedance.
The power factor is very important in power systems because it indicates how closely the effective power equals the apparent power. Power factors near one are desirable. The definition:
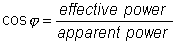
11.4 Complex Power
Complex power: S
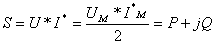
Complex power is the product of the complex effective voltage and the complex effective conjugate current. In our notation here, the conjugate is indicated by an asterisk (*).Complex power can also be computed using the peak values of the complex voltage and current, but then the result must be divided by 2. Note that complex power is applicable only to circuits with sinusoidal excitation because complex effective or peak values exist and are defined only for sinusoidal signals. The unit for complex poweris VA.
Apparent power in S is the product of the rms values of the voltage and the current, S = U*I. The unit of apparent power is VA. The apparent power is the absolute value of the complex power, so it is defined only for sinusoidal excitation.
The Power Factor (cos φ) is the cosine of the phase difference between voltage and current. It is also the cosine of the angle of the load impedance.
The power factor is very important in power systems because it indicates how closely the effective power equals the apparent power. Power factors near one are desirable. The definition:
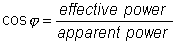
11.4 Complex Power
Complex power: S
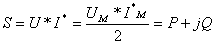
Complex power is the product of the complex effective voltage and the complex effective conjugate current. In our notation here, the conjugate is indicated by an asterisk (*).Complex power can also be computed using the peak values of the complex voltage and current, but then the result must be divided by 2. Note that complex power is applicable only to circuits with sinusoidal excitation because complex effective or peak values exist and are defined only for sinusoidal signals. The unit for complex poweris VA.

No comments:
Post a Comment