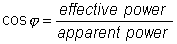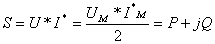He who cannot forgive others breaks the bridge over which he must pass himself.
-G. Herbert
Three-Phase AC Circuits
A single-phase (1- ) AC that is transmitted through a transmission line (consisting of a pair of wires) to a load, attention now turns to a three-phase (3- ) AC power system, in which three AC sources operate at the same frequency but with different phases. A 3- AC power system has the following advantages over a 1- AC power system:
1. The horsepower rating of three-phase motors and the KVA (kilo-voltamp) rating of three-phase transformers is about 150% greater than for single-phase motors or transformers with a similar frame size.
2. The power delivered by a single-phase system pulsates, Figure 12-1.The power falls to zero three times during each cycle. The power delivered by a three-phase circuit pulsates also, but it never falls to
zero, Figure 12-2. In a three-phase system, the power delivered to the load is the same at any instant. This produces superior operating characteristics for three-phase motors.
3. In a balanced three-phase system, the conductors need be only about 75% the size of conductors for a single-phase two-wire system of the same KVA rating. This helps offset the cost of supplying the third
conductor required by three-phase systems.
Balanced Three Phase Circuits
Single phase power has a sine wave voltage that crosses zero before reversing its polarity. In the region near the zero-crossing there is not much power. At zero there is none at all. So single phase loads often need some trickery to deliver output in this area. Often it is just the inertia of the motor or appliance.
Three phase power is always delivering power on one of its phases, and is thus preferred for generators, motors, machines and appliances that use lots of power.
If the application is large power, or small power with weight restrictions (like automobiles!) Three Phase is preferred. DC (Direct Current) is the next step up for smooth high-power devices but requires rectification, regulation and smoothing to be useful.
Another problem with DC is that, for efficient long distance transmission, it cannot be simply converted to much higher voltages than the voltage at which it was generated at the power station. Similarly DC cannot be transformed down to safer, much lower mains voltages for use by consumers.
AC (Alternating Current) is used for high power generation and distribution because it can easily be transformed, using transformers, to achieve very efficient power transmission over very long distances and can then be transformed down to low voltages for distribution to consumers.
Another problem with DC is that, for efficient long distance transmission, it cannot be simply converted to much higher voltages than the voltage at which it was generated at the power station. Similarly DC cannot be transformed down to safer, much lower mains voltages for use by consumers.
AC (Alternating Current) is used for high power generation and distribution because it can easily be transformed, using transformers, to achieve very efficient power transmission over very long distances and can then be transformed down to low voltages for distribution to consumers.
Two phase, and higher multi-phases are also used but very rarely.
Wye to wye connection
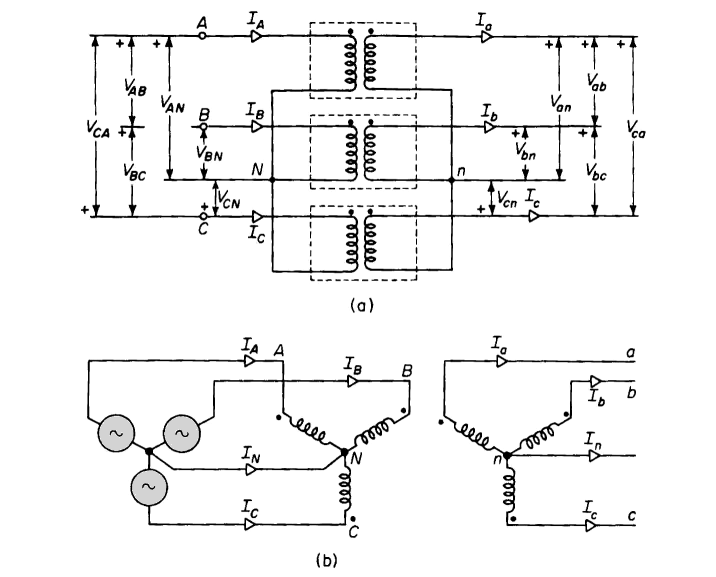
Three single-phase transformers with their primaries and secondaries both connected in wye are shown in Figs. 6-23(a) and 6-23(b). The primary neutral is shown connected to the neutral of the source and the secondary neutral connected to that coming from the load. In many applications the neutral connection consists of ground. Connecting the primary neutral to the neutral of source assures balanced line-to-neutral voltage even if the load is unbalanced or if the transformers have unequal exciting admittances. The equivalent circuits of Fig. 6-11, 6-13, and 6-14 apply to each of the three transformers connected wye-wye with or without the ideal transformer just as they do in the delta-delta arrangement. Here also, if the transformers are identical and supply balanced 3-phase load, each transformer carries one-third of the 3-phase load.
It can be seen from Fig. 6-23 that the current in the transformer winding is the line current in the wye connection. The secondary currents Ia, Ib, and Ic are therefore practically in phase with the primary currents IA, IB, and IC and if the exciting current is neglected, the current ratios are the reciprocals of the turns ratio, i.e.
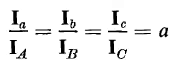 | [6-89] |
Also, if the leakage impedance is neglected, the voltage ratios equal the turns ratios, thus
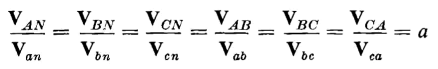 | [6-90] |
Phasor diagrams are shown for the wye-wye arrangement in Fig. 6-24. The wye connection is generally used in high-voltage applications because
 |
Wye-Delta Connection
The wye-delta connection affords the advantage of the wye-wye connection without the resulting disadvantage of unbalanced voltages and third harmonics in the line-to-neutral voltages when operating without the neutral wire. The wye-delta arrangement is shown in Fig. 6-25. In high-voltage transmission systems, the high side of a transformer bank or of a 3-phase transformer is generally connected in wye, whereas the low side is connected in delta. The delta connection assures balanced line-to-neutral voltages on the wye side whether or not there is a neutral conductor on the wye side, and it provides a path for the third harmonic components in the exciting current independent of the neutral conductor.
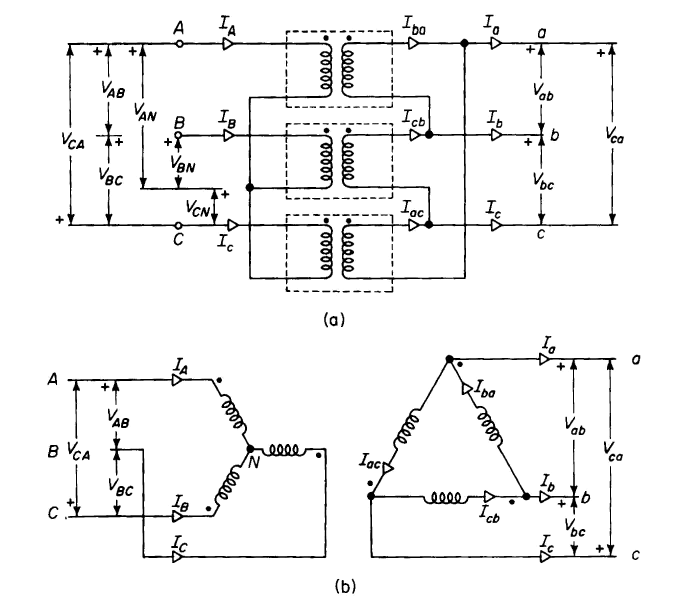 |
| Figure 6-25. Wye-delfo connection, (a) Common physical arrangement of three single-phase transformers; (b) schematic diagram. |
The wye-delta or delta-wye transformation is not confined to applications in which the high-voltage side is connected in wye, but is also coming into general use in the 208/120-v system on the low side. In such systems, the low side is connected wye with the neutral point grounded. Single-phase loads are connected line to neutral for 120-v operation, whereas 3-phase equipment, such as motors, are connected line to line for operation at 208 v.
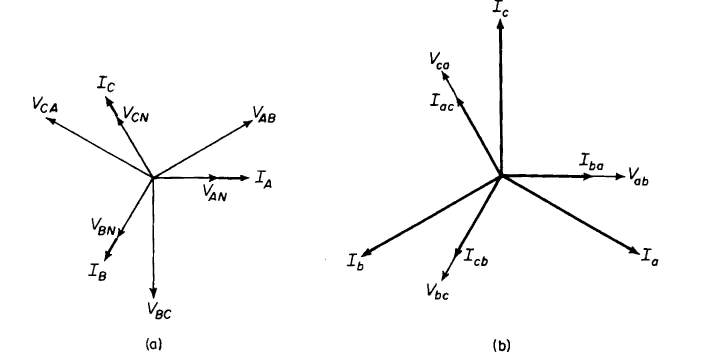 |
| Figure 6-26. Phasor diagram for wye-delta arrangement of Figure 6-25 for ideal transformers supplying balanced noninductive load, (a) Primary wye-connected; (b) secondary delta-connected. |
Figure 6-26 shows the phasor diagram for a wye-delta transformation. From this diagram it is evident that there is a large phase angle between the line-to-line voltages on the wye side and the corresponding line-to-line voltages on the delta side. This angle is 30° with the phases as designated in Fig. 6-26. Angles of 90° and 150° are possible, depending on how the phases on the two sides are designated
Delta-Delta Connection
Figure 6-21 shows three single-phase transformers, assumed to be identical, with their primaries connected in delta and their secondaries connected in delta. A common physical arrangement of the three transformers is shown in Fig. 6-21 (a); a schematic diagram typical for 3-phase delta circuits is shown in Fig. 6-21(b).
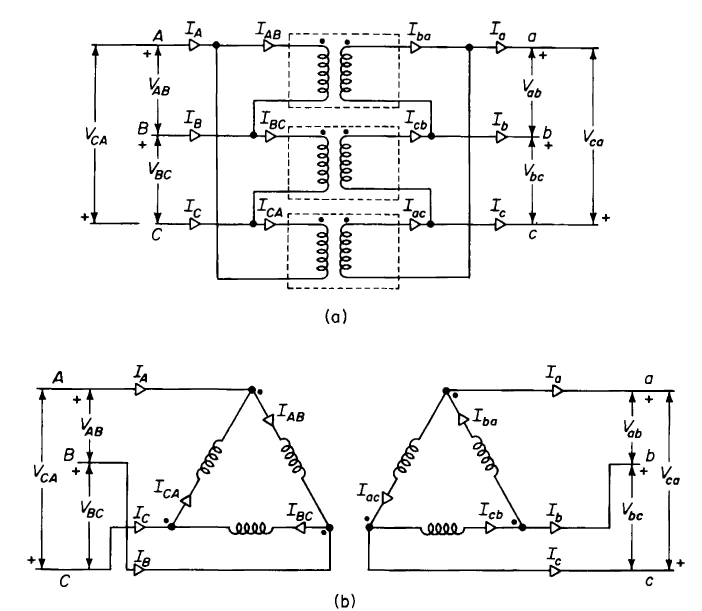 |
| Figure 6-21. Delta-delta connection, (a) Common physical arrangement of three single-phase transformers; (b) schematic diagram. |
The equivalent circuits of Figs. 6-11, 6-13, and 6-14 apply to each of the three transformers connected delta-delta with or without the ideal transformer. If the three transformers are identical and are operating under balanced 3-phase load and balanced 3-phase voltage conditions, each transformer carries one third of the 3-phase load.
It is evident from Fig. 6-21 that full line-to-line voltage exists across the windings of each transformer. Therefore, the secondary line-to-line voltages Vab, Vbc and Vca are practically in phase with the corresponding primary line-to-line voltages VAB, VBC and VCA. In addition, if the leakage impedance drops are neglected, the voltage ratios equal the turns ratio, i.e.
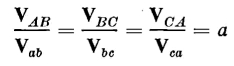 | [6-84] |
Figure 6-22 shows phasor diagrams for a bank of ideal transformers connected delta-delta and supplying a balanced unity power-factor load.
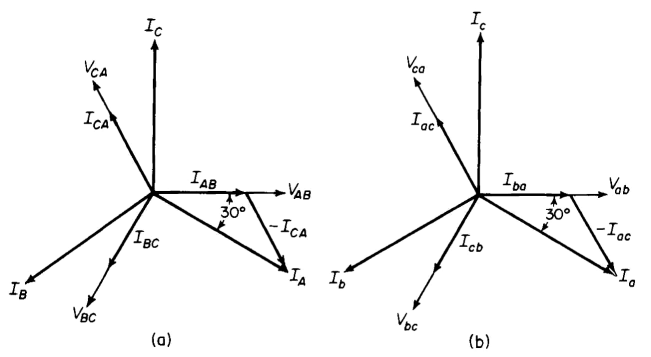 |
| Figure 6-22. Phasor diagrams for delta-delta bank of ideal transformers supplying balanced noninductive load, (a) Primary; (b) secondary. |
In the case of identical transformers, when the third harmonics in the exciting current are neglected, the line currents are  times the currents flowing in the windings under balanced conditions. This can be seen by referring to Fig. 6-21 and the phasor diagram of Fig. 6-22(a) as follows
times the currents flowing in the windings under balanced conditions. This can be seen by referring to Fig. 6-21 and the phasor diagram of Fig. 6-22(a) as follows
 times the currents flowing in the windings under balanced conditions. This can be seen by referring to Fig. 6-21 and the phasor diagram of Fig. 6-22(a) as follows
times the currents flowing in the windings under balanced conditions. This can be seen by referring to Fig. 6-21 and the phasor diagram of Fig. 6-22(a) as follows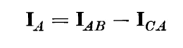
and
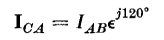
from which
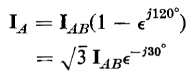 | [6-85] |
Similarly
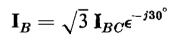 | [6-86] |
and
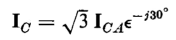 | [6-87] |
If the exciting current is neglected, then we have
 | [6-88] |
The delta-delta arrangement is restricted to applications in which neither the primary nor the secondary side requires a 3-phase neutral connection. It is generally used in moderate voltage systems because full line-to-line voltage exists across the windings, and in heavy current systems because the windings need to carry only 1/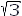 or 0.58 of the line current.
or 0.58 of the line current.
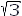 or 0.58 of the line current.
or 0.58 of the line current.